A proton in a Bainbridge mass spectrometer will draw a semicircle of a specific radius R, as presented in Figure 1.
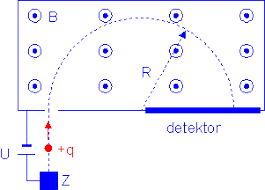
Figure 1
After calculations according to the formula
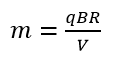
we get the mass of the proton m equal to 1.6726 x 10-27 kg.
In a Bainbridge mass spectrometer, the nucleus of deuterium (proton and neutron) will draw a semicircle of a specific radius, which after calculations gives the mass of 3.434 x 10-27 kg.
The mass of the proton and the mass of the neutron are:
1.6726 x 10-27 kg + 1.6749 x 10-27 kg = 3.3475 x 10-27 kg
3.3475 x 10-27 kg + 3.3434 x 10-27 kg = 0.0041 x 10-27 kg
Thus, the nucleus of deuterium is lighter by 0.0041 x 10-27 kg.
The mass of the helium nucleus should be exactly twice that of the deuterium nucleus, that is 6.6868 x 10-27kg. In the spectrometer, it should draw a semicircle r2 exactly twice that of the semicircle r1 drawn by the deuterium nucleus. However, this semicircle is smaller than expected (r3), as presented in Figure 2.
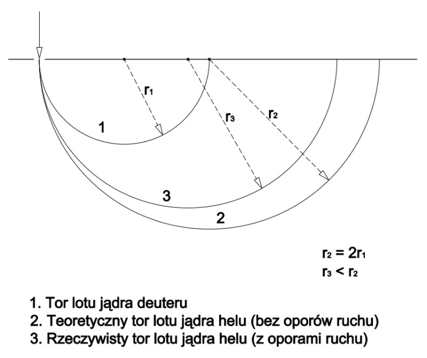
Figure 2
After calculations according to the formula
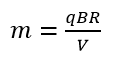
we get the mass of the helium nucleus m equal to 6.6444 x 10-27 kg.
6.6868 x 10-27 kg + 6.6444 x 10-27 kg = 0.0424 x 10-27 kg
Thus, the helium nucleus is lighter than two nuclei of deuterium by 0.0424 x 10-27 kg.
As it is seen, in nuclei bigger than proton, the mass “disappears” somewhere. Thus, “the mass deficiency” occurs. What happened with it? According to physicists, the mass was converted into binding energy of individual nucleons in the nucleus.
How? It is not known.
The above problem is explained in a classical way by Model 31. It follows from the model that atoms do not move in a vacuum but in quantum gas. Classical physics says that bodies moving in gas are subject to resistance to motion.
It is seen from the formula for the resistance force D
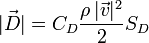
that, among others, it is proportional to SD the area of projection of a body (an atom) onto a plane perpendicular to the direction of the motion (“the area of resistance”), and to CD the coefficient of the resistance force (“the shape factor”).

In contrast to modern physics, Model 31 presents the shapes of proton, neutron, and the atomic nuclei built of them. It will be reasonable to consider how these shapes affect the amount of the resistance force.
According to Model 31, a proton has a shape similar to a cylinder (see Figure 3).
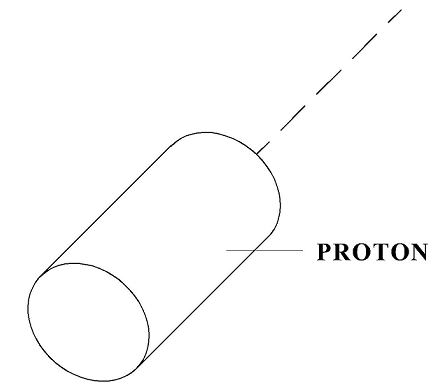
Figure 3
According to the formula for the resistance force, its resistance during motion in “a vacuum”, that is in non-existent for physicists quantum gas, will be proportional to the specified SD (“area of resistance”) and to the specified resistance factor CD. As shown above, in a Bainbridge mass spectrometer, this nucleus will draw a semicircle of a specific radius, which after calculations gives the mass of 1.6726 x 10-27 kg.
Let us take into account a deuterium nucleus. It consists of a proton and neutron and, according to Model 31, it has a shape of two connected cylinders (see Figure 4).
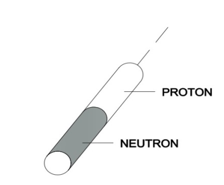
Figure 4
Compared to a proton, a cylinder of this shape has a greater “area of resistance” and a larger shape factor (resulting from the fact that a deuterium cylinder is twice as high as a proton cylinder). According to this, the resistance force caused by the nucleus of deuterium during motion in quantum gas will be greater. Therefore, the nucleus of deuterium in a Bainbridge mass spectrometer will not draw a semicircle proportional to the sum of the proton and neutron masses (m2), but due to resistance to motion it will be a semicircle of a smaller radius (m1), as presented in Figure 5.
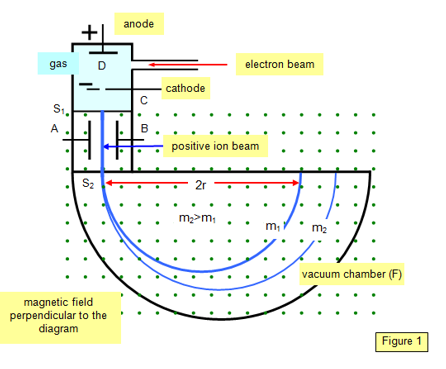
Figure 5
A smaller radius r of the semicircle in the formula
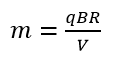
means a smaller mass of the deuterium nucleus ( ). Thus, the mass did not disappeared but the nucleus of deuterium, as a result of increased resistance to motion, drew a smaller circle than expected.
NOTICE:
The mass of the nucleus is never measured experimentally. The mass of the nucleus of a particular element is always calculated on the basis of the value of the radius drawn by the nucleus in the spectrometer.
Physicists assume that a smaller radius means a smaller nucleus mass.
Physicists do not accept that a smaller radius mans larger resistance to motion of the nucleus, which is in motion in the ubiquitous quantum gas.
Let us take into account a helium nucleus. It consists of two deuterium nuclei and, according to Model 31, it has a shape of two connected cylinders (see Figure 6).
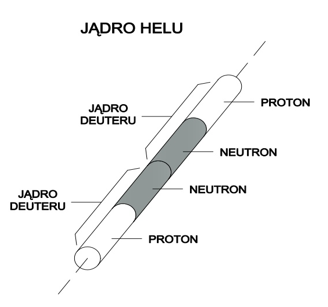
Figure 6
Compared to a nucleus of deuterium, a cylinder of this shape has twice as large “area of resistance” and a larger shape factor (resulting from the fact that a helium nucleus cylinder is twice as high as a deuterium nucleus cylinder). According to this, the resistance force caused by the nucleus of helium during motion in quantum gas will be much greater when compared to the resistance force of the nucleus of deuterium.
Therefore, the nucleus of helium in a Bainbridge mass spectrometer will not draw a semicircle proportional to its mass, but due to resistance to motion it will be a semicircle of a smaller radius. A smaller radius r in the formula
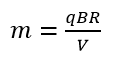
means a smaller mass m of the helium nucleus.
Such a scheme will repeat itself for all the remaining nuclei which occur in nature. With an increase in the number of nucleons in the nucleus, its area of resistance and the resistance to motion coefficient will increase, which will result in increased resistance to motion of the nucleus, that is a smaller than expected semicircle radius r in the spectrometer and a smaller than expected calculated nucleus mass m.
Thus, the actual increase in resistance to motion of consecutive larger and larger nuclei manifests itself in the virtual loss of mass of these nuclei calculated by physicists according to the formula:
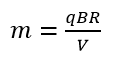
This actual increase in resistance to motion of the nuclei is formulated by physicists as the virtual loss of mass of the nuclei in kilograms (kg) or atomic mass units (u), or megaelectron volts (MeV), or in joules (J) as follows:
1.6605 x 10-27 kg = 1u = 931.44 MeV = 1.492,16 x 10-10 J
Below we will present the actual increase in resistance to motion of first few nuclei expressed in the virtual loss of mass in kilograms.
The virtual mass “deficiency” is:
For the deuterium nucleus – 0.0041 x 10-27 kg,
For the helium3 nucleus – 0.0119 x 10-27 kg
For the helium4 nucleus – 0.0500 x 10-27 kg
For the lithium6 nucleus – 0.0544 x 10-27 kg
For the beryllium8 nucleus – 0.1007 x 10-27 kg
For the boron10 nucleus – 0.1154 x 10-27 kg
For the carbon12 nucleus – 0.1108 x 10-27 kg
For the nitrogen14 nucleus – 0.1866 x 10-27 kg
For the oxygen16 nucleus – 0.2275 x 10-27 kg
For the (uranium238) nucleus, the virtual deficiency of mass is 3.2133 x 10-27 kg.
In the above, It can be clearly seen an enormous, relative increase in the mass “deficiency” (of resistance to motion) for the first three nuclear nuclei (of deuterium, helium3, and helium4). What is the reason for this? In order to explain this, let us compare the shapes of these nuclei (see Figure 7).
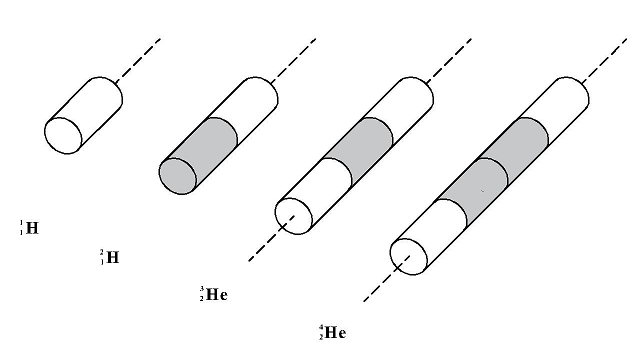
Figure 7
The first nucleus (proton) has a shape of a cylinder. The next nuclei (of deuterium, helium3, and helium4) have a shape of a cylinder of the same diameter but two, three, and four times higher than the proton cylinder. If we delve into considerations on the dependence of the resistance coefficient CD on the shape of the body that resists, we will see that for a cylinder this coefficient increases rapidly with the increase in its height. And here is the key to the riddle. Large differences in the resistance coefficients for the three first nuclei cause proportional differences in resistance to motion of these nuclei when their mass is being measured, which results in physicists calculating large differences in the virtual mass deficiencies of these nuclei.
The nuclei of the next atoms, like lithium6, carbon12, fluorine16 in Figure 8 and the following, are not significantly different in shape as those in Figure 7. These nuclei are formed in such a way that the consecutive cylinders (deuteron or helions) “are glued to each other” from a side, so the “length” of the cylinders of the atomic nuclei does not change (see Figure 8).
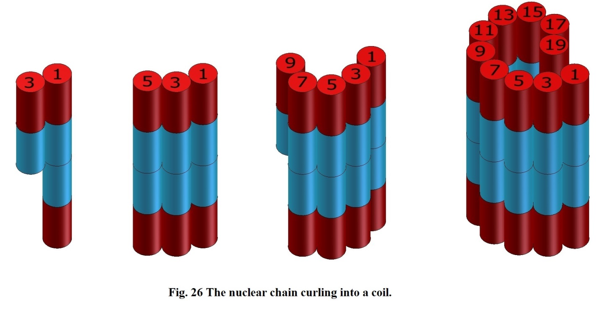
Figure 8
That is why physicists are calculating mass deficiencies of these nuclei, which are less and less different from one another.
Now we are able to answer the question from the title of this note.
A Bainbridge mass spectrometer (and any other one) is used to measure resistance to motion of an atomic nucleus moving in quantum gas.
Now we can also say what is actually presented by the curve of binding energy depending on the number of nucleons in the nucleus as shown in Figure 9.

Figure 9
This curve presents measured in a Bainbridge mass spectrometer and expressed in MeV resistance to motion of the nuclei of individual elements divided by the number of nucleons included in a particular nucleus. In other words, this curve has no physical sense, because it shows resistance to motion of the nucleus for a single nucleon.
Here once again, we can see how far-reaching are the effects of the lack of knowledge that, in parallel with the world of atoms, there exists the world of energy quanta, which creates resistance to motion for the atoms.
Let us come back again to the formula for the resistance force
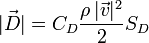
There is the quantity ϱ which means the density of gas. An atom moves in quantum gas. An indicator of the density of quantum gas is the temperature. The lower the temperature, the lower the density of quantum gas. A lower density of quantum gas means less resistance to motion of an atomic nucleus, while less resistance to motion means a larger radius drawn by the nucleus in the spectrometer, which in turn means a calculation from the formula
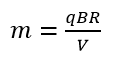
of a larger mass of the nucleus. The above means that it is enough to measure the mass of a proton at a temperature significantly lower than room temperature (like the temperature of liquid nitrogen) to see that the mass of a proton is not a physical constant but a material constant (depending on the measurement temperature).

