SUMMARY
On the basis the classical physics it has been shown that an increase in the mass of ions in accelerators and a decrease in the mass of ions in spectrometers is virtual. There has been proposed a crucial experiment (experimentum crucis) to check the validity of these observations.
Galileo’s principle of gravity concluded that in a uniform gravitational field, where there is no resistance to motion, all bodies move with the same acceleration regardless of their mass. This means that it is not possible to use the gravitational field for dynamic determination of the mass of bodies. In fact, it is true. Let us now take into account a uniform electric or magnetic field. Since all kinds of fields are subject to the same dependencies presented in the following formula
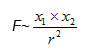
for these fields, there should be applied the above principle that in a uniform electric or magnetic field, where there is no resistance to motion, it is not possible to use these fields for dynamic determination of the mass of bodies. Actually, it is not true. Physicists use these fields for determining the mass of atoms, particles, and elementary particles. Is this a fault?
We will try to show that it is. Here is a helpful notation of not directly presented above Galileo’s principle of gravity in relation to the electric or magnetic field. It reads as follows. If in a uniform electric or magnetic field various bodies move with different accelerations dependent on their mass, this means that resistances to motion are present in this field. We know that in the mentioned above fields charged particles move with different accelerations dependent on their mass. It can be concluded that the charged particles which are moving in these fields are subject to resistances to motion. Where do they come from? It is explained in Model 31.
To atoms, the space around them is not a vacuum. They are in motion in ubiquitous quantum gas. Atoms are so small that quantum gas makes a significant resistance to their motion, just like the air makes a resistance to the motion of big bodies.
If the moving atoms are subject to resistance to motion, in the considerations about them the resistance force should be taken into account:

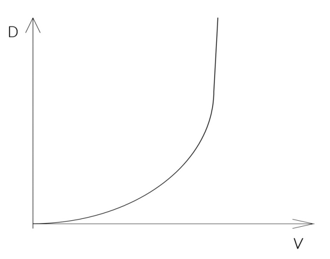
As it is apparent from the above, the resistance force is proportional to the square of the velocity of an atom in motion.
D ~ v2
For example, in an accelerator a tenfold increase in velocity of an atom (ion) results in a hundredfold increase in resistances to motion. Therefore, an acceleration of particles to higher and higher velocities requires a supply of disproportionately larger portions of energy and, at some point, an acceleration of a particle over a certain velocity becomes impossible. This is a phenomenon commonly know in the classical physics and everyday life. For instance, the operation of parachute is based on this phenomenon. The above dependencies are presented in the figure below.
Not seeing the existence of quantum gas, physicists think that accelerated atoms move with no resistance to motion. They had to explain the above results in another way. The idea was developed that with an increase in the velocity of an atom, its mass is increasing. How? It is not known. Hendrik Antoon Lorentz created a special mathematical structure called the Lorentz factor,
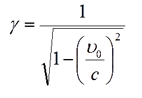
which enabled to calculate thin new kind of mass.
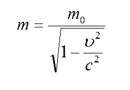
The above considerations are illustrated in the figure below.
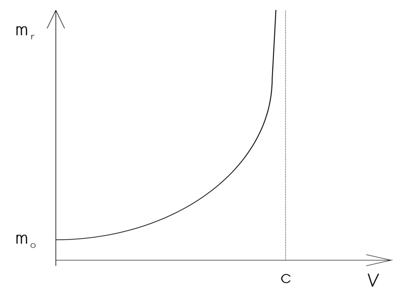
Let us now compare both diagrams.
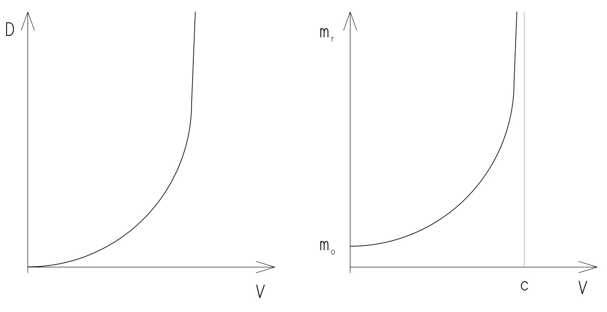
As seen, they are practically identical. The first of them has been derived from Model 31 and is based on the classical physics. The other one was made after the limit C and the completely abstract Lorentz factor were arbitrarily introduced to the physics. It was only this combination which enabled to introduce to the physics a new, controversial being, so-called relativistic mass mr. Relativistic mass was introduced to the physics ad hoc, only in order to explain the phenomenon which physicists had not been able to explain in a direct way.
Difficulties in explaining this and other phenomena, resulting from the lack of awareness that in parallel with the world of atoms, there exists the world of energy quanta, gave rise to the physics alternative to the classical physics, which was named relativistic physics and considered superior to the classical physics.
From the formula for the resistance force D it can be concluded that it is proportional to SD the area of projection of an atom onto a plane perpendicular to the direction of the motion (“the area of resistance”), and to CD the coefficient of the resistance force (“the shape factor”).
D ~ SD CD
Since Model 31 presents the shapes of proton, neutron, and the atomic nuclei built on them, it will be reasonable to consider how these shapes affect the amount of the resistance force. Let us take into account a deuterium nucleus. It consists of a proton and neutron and, according to Model 31, it has a shape of two connected cylinders.
DEUTERIUM NUCLEUS
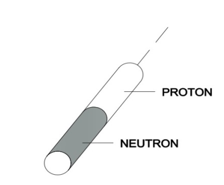
In a Bainbridge mass spectrometer, this nucleus will draw a semicircle of a specific radius, which after calculations gives the mass of 3.3434*10-27 kg. Let us take into account a helium nucleus. It consists of two deuterium nuclei and, according to Model 31, it has a shape of four connected cylinders.
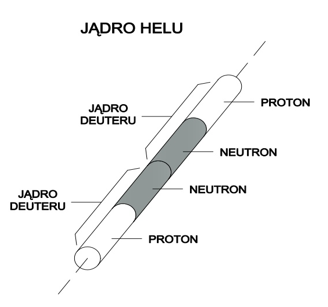
The mass of the helium nucleus should be exactly twice that of the deuterium nucleus, that is 6.6868*10-27 kg. In the spectrometer it should draw a semicircle exactly twice that of the deuterium nucleus. However, this semicircle is smaller than expected and after calculations it gives the mass of 6.6444*10-27 kg. It means a decrease of 0.0424*10-27 kg. In other words, “the mass excess” occurred. What happened with it? A new theory must have been created. According to physicists, the mass was converted into binding energy of individual nucleons in the nucleus. How? It is not known. Model 31 explains the above result in a classical way. In the spectrometer the atomic nuclei are subject to resistance to motion. The helium nucleus has a larger “area of resistance” SD and a larger “shape factor” CD than the deuterium nucleus. It results in the fact that the force of resistance to motion of the helium nucleus in the spectrometer will be larger than the force of resistance to motion of the deuterium nucleus. If the resistance force is larger, the nucleus will draw a semicircle smaller than expected. The mass of the components of the nucleus (protons and neutrons) remained unchanged; what changed (increased) was only the resistances to motion, resulting from an increase in “the area of resistance” of the nucleus and its “shape factor”. The above considerations are illustrated in the figure below.

The previous considerations can be summarised as follows. There are two apparatuses – an accelerator and a mass spectrometer. For the same particle, physicists confirm an increase in the mass in the accelerator, while in the spectrometer a decrease in the mass. Only common for the two phenomena is that it is not known how they occur. Model 31 simply, clearly and logically explains the two phenomena in terms of the classical physics.
As seen from the formula for the resistance force, it is proportional to the density of quantum gas.
D ~ q
Quantum gas is the heat. The concentration, “density” of quantum gas is the temperature. The density of quantum gas is proportional to the temperature.
q ~ T
It follows that for atoms, resistances to motion in quantum gas are proportional to the temperature.
D ~ T
How can the validity of these considerations be tested? Let us take into account a Bainbridge mass spectrometer.
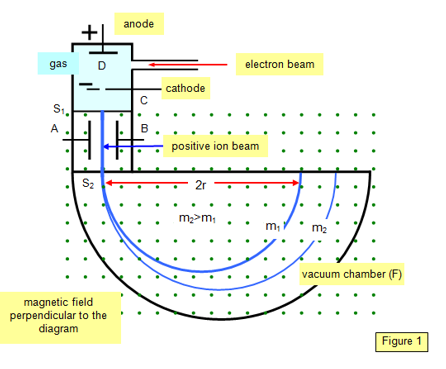
In this spectrometer, the mass of ion (m1) is determined in the temperature about 293 K (200 C). It is determined in an indirect way by measuring the radius of a semicircle r drawn by a ion in the area of the magnetic field, while the calculated mass is proportional to the measured radius.
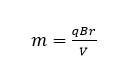
m – mass of ion,
q – charge of ion,
B – magnetic induction,
r – radius of a semicircle drawn by a ion in the area of the magnetic field,
V – velocity of ion.
If we determine the mass of the same ion in the temperature of, for example, liquid nitrogen (77 K), it will move with the same velocity as before into the area of the magnetic field with a lower density of quantum gas, which means that it will be subject to lower resistances to motion, that is, it will draw a larger semicircle in the magnetic field, which means that its LARGER mass (m2) will be calculated.
In the light of the above, we will have to accept that the mass of atoms is dependent on the temperature of the determination.
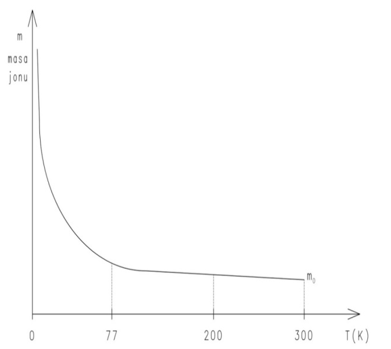
A confirmation of the results of the experiment presented above will be an experimentum crucis, that is indisputable evidence of the validity for the above assumptions that:
– atoms move in quantum gas,
– quantum gas makes resistance to motion for the atoms moving in it,
– resistance to motion for the atoms moving in quantum gas are proportional to the density of the gas, that is to its temperature.
This experiment can be performed only by physicists, and nobody will force physicists to perform it.
The summary of all above considerations is the statement that:
– fields existing in nature (gravitational, electric, magnetic) cannot be used for dynamic determination of the mass of bodies, atoms, particles, or elementary particles.
In other words, practically we do not know what are the real masses of atoms, particles, elementary particles.
Now, it is clearly seen what error is made by physicists while measuring the masses of atoms. Since they are not able to determine the masses directly in the static way (atoms cannot be weighed because they are in constant motion), they determine the masses in an indirect way, dynamically.
The measurement is made of the flight range of an atom (ion) launched into the magnetic field with a certain velocity, and on this basis its mass is calculated. It is the same as calculating the mass of a cannonball in the gravitational field on the basis of the range of its flight after being fired from a cannon. The experiment shows that such results are unreliable because the range of the ball depends on, among others, the density of the air (the air resistance to motion). The efficiency of this method (repeatability of atomic mass measurements) is apparent and dependent on the fact that the measurements are always mad ein the same temperature, with a constant density of quantum gas, which means constant resistances to motion in the gas. However, if the temperature of measurement is changed, the density of quantum gas changes (its resistances to motion change) and the whole the whole elaborate method of mass measurement collapses.
In order to rescue at least a part of this “fallen mass”, with calculated masses of atoms, particles, and elementary particles, physicists will have to add that this is the mass determined for the specific temperature (200 C). Now, this is how they are already doing it for a lot of other physical quantities, like for the specific heat capacity. But how, then, to classify the mass of the proton or electron as universal physical constants?

