ABSTRACT
It has been shown through several examples that the application of mathematics to the phenomena whose nature is not known may lead physics to a dead end.
Aristotle maintained that “the primary task of natural science is to find the essence of each thing, that is to reach the essence of the matter, because only knowing the essence of a thing, a further knowledge about it can be reliably derived”.
Galileo considered the task thus understood to be impossible and claimed that it is only real to describe the features of the observed phenomena, and they should be features expressed mathematically. Consistent mathematization of physics means giving up a search for the essence of a thing. In contemporary physics this view is valid in its entirety.
Below are a few examples of how such a mathematized approach to science leads physics astray.
Example 1.
Let us compare two formulas:

Both of the above formulas are mathematically correct. The dimensions of the components of the both formulas are identical [m] ,[] ,[s] but the physical sense of the both formulas is different.
According to the first formula, the length of the electromagnetic wave depends only on its frequency because its velocity is constant. The lower the frequency of the electromagnetic wave, the greater its length. At high frequencies of the order of billions of vibrations per second everything looks normal. The lengths of the waves are of the order of nanometers. It is easy to imagine a light wave with the frequency of vibrations of the order of billions of hertz and the length of the order of several hundred nanometers. It belongs to a microworld. However, when lowering the frequency, problems appear. An electromagnetic wave with the frequency of vibrations of the order of a few hertz has a length of the order of tens of thousands of kilometers. Thus, a subatomic electromagnetic wave, when lowering its frequency, grows to a simply astronomical size? How?
According to this formula, with the wave frequency of 1 Hz, an electromagnetic wave is formed with the length of almost three hundred million meters. In other words, if the human brain produces electromagnetic waves with the frequency of 1 – 30 Hz, it means that it works at a wavelength of 10 – 300 million meters. It is impossible to understand. Thinking must be turned off here.
So, where is the mistake? The mistake is that the frequency of vibrations does not always have to be associated with a wave. Likewise, each oscillator has a frequency of vibrations. An oscillator moving in space has also a velocity, another property attributed to a wave. An oscillator, however, having even two properties of a wave (frequency and velocity) is still not a wave but a moving, vibrating particle. And, if the velocity of such a vibrating particle is divided by the frequency of its vibrations, then, although from the mathematical point of view everything will be alright, we will not obtain the wavelength of this particle (since it is not a wave), but the nonsense described above will come out.
According to the second formula, within 1 s a corpuscle vibrating with the frequency will travel a distance of nearly three hundred million meters. This is normal and understandable. This only means that a quantum of energy vibrating with a defined frequency moves at the speed of 299792458 m/s.
Example 2.
According to Model 31, the foundation of the world of quanta is kinetic energy stability of these quanta.

If the Planck constant means the kinetic energy of the quantum, it has the dimension of energy [J] and has the value
h = 6,62 x 10-34 J
Thus, the commonly know mathematical product hv will have the dimension that is it will have the dimension of the power unit, watt .
This results with the fact that the commonly known product hv means the quantum power, not its energy. The power is expressed by the formula
P = hv
P – quantum of energy power,
h = 6,62 x 10-34 J the Planck constant,
v – frequency of vibrations of energy quantum.
Thus, the power of energy quanta depends on the frequency of their vibrations.
A quantum vibrating with the frequency of 1 Hz has the power 6,62 x 10-34 W (it is like a pneumatic hammer), while a quantum vibrating with the frequency of 1 MHz has the power a million times greater 6,62 x 10-28 W (it is like a flying pneumatic hammer). However, within one second the both quanta travel the same distance, that is 299 792 458 m, and they have the same kinetic energy of 6,62 x 10-34 J . The quantum vibrating with the frequency of 1 Hz is not a wave with wavelength of ~300 000 000 m, and the quantum vibrating with the frequency of 1 MHz is not a wave with wavelength of ~300 m. The both quanta are corpuscles, and their lengths L are slightly different (see figure below).

A quantum of energy is an eternally moving in space and eternally vibrating oscillator. This oscillator always moves at a constant speed c, while the frequencies of its vibrations can be various. If it hits us, how we feel the hit depends on the frequencies of its vibrations, its power, and not on its kinetic energy because this is always the same. Therefore, a quantum of gamma radiation devastates our body, while a quantum of radio radiation does not do us any harm. Therefore, a quantum of UV radiation knocks electrons out from the surface of metal, while a quantum of IR radiation is not able to do it.
If we know the kinetic energy of the energy quantum, we can calculate the mass of the energy quantum.
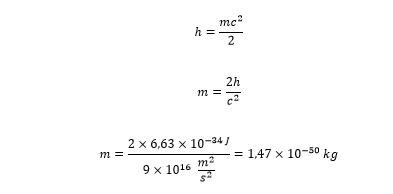
These are the conclusions drawn from Model 31, that is the “Aristotelian” approach to physics.
And now the “Galilean” approach, which means an application of mathematics without knowing what a quantum of energy is.
In this approach, the formula is applied
E = hv
E – quantum of energy [J],
h = 6,62 x 10-34 Js – the Planck constant,
v – frequency of vibrations of energy quantum [1/s].
This formula is not good because, being a corpuscle, a quantum of energy always moving at a constant speed cannot have various kinetic energies. This formula violates basic physics.
Robert Andrews Millikan, determining the Planck constant, measured the energy of electrons knocked out from metal depending on the frequency of vibrations (power) of quanta, and not depending on the energy of quanta. Kinetic energy of these quanta has always been the same and it should have been calculated as the Planck constant after Millikan had carried out his experiment. The calculation would be expressed in joules and have the value 6,62 x 10-34 J . Because then it was wrongly assumed that the kinetic energy of knocked out electrons was a result of the kinetic energy of the energy quanta, Millikan calculated a completely incomprehensible Planck constant with the dimension [J x s] . Unhappily, the dimension [J x s] , after having been dissected, has a physical sense (it is a dimension of angular momentum), which strengthened the physicists in their misconception that they were on the right track. Thus arose the statement that “each elementary particle has it own internal angular momentum, which by no means should be identified with the classical concept of angular momentum and we need not ask what this own internal angular momentum actually is”.
Example 3.
The mass of an alpha particle should be twice that of the deuterium nucleus, that is
m0= 6.6868*10-27 kg.
Here we have a formula for the mass in special relativity:
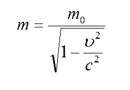
This results with the fact that for an alpha particle, at a certain velocity of ion in an accelerator, we will calculate the mass greater than expected 6.6868*10-27 kg.
m > m0
Thus, we have a formula for the mass of ion in the mass spectrometer.
m =
After putting the appropriate values into the formula, it results that the mass of the alpha particle is smaller than expected ( 6.6444*10-27 kg, instead of 6.6868*10-27 kg).
m < m0
So, there are two research apparatuses – an ion accelerator and an ion mass spectrometer. In the both apparatuses a given ion is accelerated to the same speed. For the accelerator, after putting the data into the formula, we calculate (determine?) an increase in the mass of the given ion. For the spectrometer, after putting the data into the formula, we calculate (determine?) the mass excess of the same ion. Therefore, depending on the apparatus, an increase in the mass or the mass excess of the same ion is determined. It seems strange, therefore it would be worthwhile to know how this happens. Physicists, in accordance with the doctrine of Galileo, do not even try to go into the essence of the phenomena. Model 31, in accordance with the doctrine of Aristotle, assuming the existence of the subatomic level of the organization of matter (quantum gas), explains both of these mathematical anomalies by the fact that moving atoms (ions) are subject to resistance to motion created by quantum gas. The details of this issue are presented in the note “WE SHOW THAT DETERMINING THE MASS OF ATOMS, ELEMENTARY PARTICLES IS AN UNSOLVED PROBLEM”.

