The structure of an atom of hydrogen is very similar to a free neutron (see Figure 1).
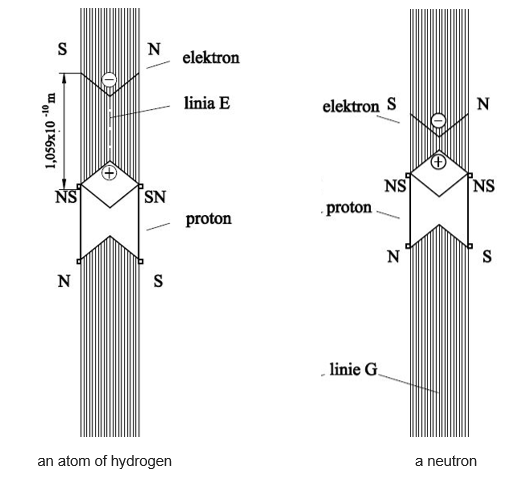
Figure 1
They are both electric dipoles with different dipole moments. The distance of an electron from proton in the hydrogen atom is 1.059 x 10-10 m, which gives a dipole moment of 1.059 x 10-10 e x m. In a neutron, the distance of an electron from proton is smaller than 1.09 x 10-14m, but the exact value is still undetermined. The value 1.09 x 10-14 m is the distance of the first electron in the uranium atom from proton, the smallest occurring in nature distance of an electron from proton in an atom (this is the exact value).
If the structure of a neutron is close to that of an atom of hydrogen, it would be reasonable to examine the ionization energy of the neutron, and then to calculate the distance of an electron from proton in the neutron, and the electric moment of the neutron. Already over a hundred years ago, physicists measured all ionization energies of all atoms in the periodic table. The tests were completed at this stage. We must come back to these tests and try to ionize the neutron. To do this, after a given atom, e.g. xenon, has been stripped of all electrons (+54Xe), the voltage should be further increased to the limits of possibility. If, at a certain voltage, ionization current occurs, it must be noted and then the distance of an electron from proton in the neutron must be calculated form the classic Coulomb’s law. If the chances of an increase in the voltage expire, and ionization current does not occur, it will be possible to say that in the neutron, the distance of an electron from proton is smaller than… (now we give the value calculated form the classic Coulomb’s law).
Here are examples of calculations.
- Let us assume that ionization current occurs at 1 530 000 V. This means that the distance of an electron from proton in the neutron is 0.094 x 10-14 m.
- The maximum voltage reached is 3 100 000 V. Ionization current has not occurred. This means that the distance of an electron from proton in the neutron is smaller than 0.046 x 10-14 m.
Neutrons in atoms move at a speed of several hundred meters per second, while a free neutron moves at a speed of 22 000 000 m/s. Probably this speed is the cause of instability of a free neutron. A free neutron, moving in quantum gas at a speed tens of thousands of times greater than a combined neutron in an atomic nucleus, is subject to such a great resistance to motion that it decays into proton and electron.
Another example of the similarity of construction of a neutron and atom of hydrogen is the following fact. Four in a million occurrences does not end with a free neutron decay, but an atom of hydrogen is created. In these cases, an electron does not break off but it is moved away from the proton to a distance of 1.059 x 10-10 m, so the neutron, becoming a hydrogen atom, is able to slow down to a speed of several hundred meters per second.
The whole matter of the Universe is composed of electric dipoles, which form atoms. Dipole matter (atoms) in their motion in quantum gas create such powerful resistances that they can reduce their speed to several hundred meters per second. This reduction in speed made it possible for solids, liquids and gases to be formed from atoms. Non-dipole matter (atomic nuclei), that is dipoles without electrons, in their motion in quantum gas create such small resistances that they have to move at speeds of the order of tens of thousands of kilometers per second.
This is why an atom of helium (dipole particle) moves at the speed of about 500 m/s, while a helium nucleus (alpha particle), that is a non-dipole particle, moves at the speed of 15 000 000 m/s.
The above is a direct powerful evidence for the existence of the subatomic world of energy quanta, which creates resistances to motion for the particles moving in this world.
Finally, we will show how presented in Figure 1 an atom of hydrogen and neutron combine and form a deuterium atom (see Figure 2).
G – gravitational field lines
Figure 2

