ABSTRACT
On the basis of classical physics a gravitational charge carrier was found, uniformity of all types of fields (electric, magnetic, and gravitational) was obtained, and on this basis the problem of inertial and gravitational mass equivalence was solved in theory.
We encounter the concept of mass twice: first – while formulating the second law of motion, second – while describing gravitational forces. In the first case, we treat mass as a measure of inertia of the body, in the second, as a measure of its ability of a mutual attraction with another body having mass. It was experimentally determined that both those masses are equivalent but it has never been explained in theory why.
It is known that bodies have electric or magnetic charges which generate electric or magnetic fields. Bodies with charges attract or repel each other. This attractive or repulsive force depends on the number of charges.
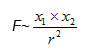
F – force of interaction,
x – amount of interaction-inducing charge carriers,
r – interaction-inducing charge distance.
The third type of field, gravitational field, is significantly different from the fields mentioned above. The force of gravitational interaction, instead of depending on the amount of gravitational charges, depends on the mass of the body.
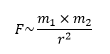
F – force of interaction,
m – masses of bodies,
r – bodies distance
It can be seen with the naked eye that something is not right here. Logic dictates that electrostatic, magnetic, and gravitational interactions subjected to the same dependencies should be free from such anomalies. In other words, gravitational charge carriers in the mass body should be found, and then everything will become clear, simple and logical.
In the study “Step by Step to Model 31” it was shown how gravity emerges. The final conclusion of this argumentation is that an elementary gravitational charge carrier is proton. This simple conclusion results in the fact that the above mentioned difference between electric, magnetic, and gravitational interactions disappears immediately.
For the electrostatic field, to the formula 1), x shall represent the quantities of electrons or positrons inducing electrostatic charges in the particular bodies.
For the gravitational field, to the formula 1), x shall represent the quantities of protons inducing gravitational charges in the particular bodies.
It only remains to explain why substitution of masses of bodies to the formula for the gravitational force also satisfies the dependency presented in the formula 1. To explain this, it will be helpful to use the arguments about the structure of an atom included in the study “Step by Step to Model 31”.
An atom is composed of the nucleus and electrons. Atomic nuclei are composed of neutrons and protons. Neutrons are protons with electrostatic charges neutralized by electrons located very close to those protons and at equal distance from them. Electrostatic charges of the remaining protons have been neutralized by electrons located at various distances from those protons. Below is an example of an argon atom with visible the above-mentioned two types of neutralized protons.
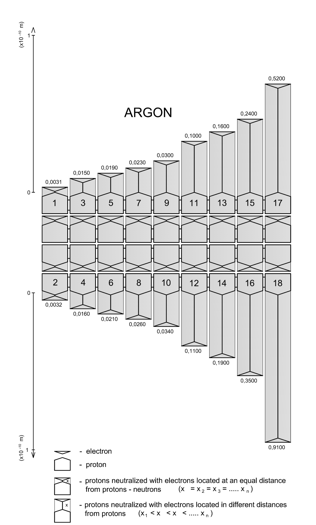

Until now it has been known that each atom is composed of protons, neutrons, and electrons. Now, the above can be simplified by stating that:
each atom in the universe is composed of neutralized protons and each of those neutralized protons is a carrier of elementary charge of the electron.
Since each body is composed of atoms, all bodies in the universe are composed of neutralized atoms, which means that all bodies are gravitational charge carriers. A question arises why they are neutralized protons? According to Model 31, a proton as an elementary gravitational charge is at the same time a carrier of an elementary, positive electrostatic charge. The force of interaction of an electrostatic charge is several dozen orders of magnitude greater than the force of gravitational interaction. Therefore, in order for the gravitational interaction of a proton to reveal, its electrostatic charge has to be neutralized. It is realised by neutralizing a positive charge of a positron with a negative charge of an electron.
In the light of the above, we should properly write as follows.
For the electrostatic field, to the formula 1), x1 and x2 shall represent the quantities of electrons or positrons inducing electrostatic charges in the particular bodies.
For the gravitational field, to the formula 1), x1 and x2 shall represent the quantities of neutralized protons inducing gravitational charges in the particular bodies.
Since the sum of the masses of protons neutralized in an atom is the exact mass of this atom, we can assume that a neutralized proton is at the same time an elementary mass unit.
In the way described above, an equivalence of the three types of fields (gravitational, electric, and magnetic) was gained, which has not occurred so far. Moreover, it was explained in theory, existing for three hundred years, the problem of two masses equivalence in Newton’s equations

Gravitational mass and inertial mass are equivalent because the neutralized proton, being an elementary gravitational charge, is at the same time an elementary mass unit.
In the light of the above, a gravitational charge can be found much faster on the basis of simple reasoning.
Newton and Coulomb’s equations
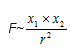
show that all types of fields (gravitational, electric, and magnetic) are subject to the same dependencies.
It means that all types of fields have elementary charges.
Thus, the gravitational field also has elementary charges.
If the gravitational force depends exactly on the mass of the body, it means that an elementary gravitational charge is an elementary unit of the mass of the body.
An elementary unit of the mass of the body is a neutralized proton.
Thus, an elementary gravitational charge is a neutralized proton.

